One of the teams here at Atlassian has been working on an eventsrc backend for their application. The API for the storage backend looks like:
trait EventStorage[F[_], K, S, E] { self =>
def get(key: K, fromSeq: Option[S]): Process[F, Event[K, S, E]]
def put(event: Event[K, S, E]): F[EventStreamError / Event[K, S, E]]
def latest(key: K): OptionT[F, Event[K, S, E]]
}
In English, the methods are for:
- Getting a stream of events, filtered by their key
- Creating an event
- Getting the latest event
The team needed a way of taking two storage backends and getting a new storage backend which:
- Gets events from both streams, merging the sorted streams together by event keys
- Creates an event in the designated “primary” store
- Gets the latest event (probably would be in primary but could be in secondary if an error happened)
The implementation was a bit tricky and relied on Tee from scalaz-stream. You might want to take a look at the code (specifically, take a quick look at the merge function) before reading on.
Coincidentally, the team I work on also needed this feature a few months after it was implemented. My job was to take their work and put it back into the eventsrc project so that we could reuse it.
I’ve used scalaz-stream for a few years but I’m always confused by how Tee and Wye work. The original project had some useful integration tests for the dual storage, which I was happy to trust, but I prefer to write property-based unit tests for algebraic properties as much as I can.
I spent a while looking at the signature:
def combine[F[_]: Monad, K, S: Order, E](
primary: EventStorage[F, K, S, E],
secondary: EventStorage[F, K, S, E]
): EventStorage[F, K, S, E]
If you ignore the specifics, you might be able to see it looks a bit like:
(A, A) => A
Which is the same signature as the append operation on scalaz.Semigroup. The operation has the following law:
append(append(a, b), c) = append(a, append(b, c))
Which is known as the associativity law. Could we turn our “combine” method into a Semigroup? That is, did the method uphold this law?
To answer this, we need to think about what it means for instances of our storage API to be equal. Since we have 3 methods on the API, an instance is equal to another if it gives the same results as the other for each of the methods.
It is easy to see that this would be true for the “put” and “latest” methods. With “put” we just use the first storage and we can see that it’s associative:
first(first(a, b), c) = a
first(a, first(b, c)) = a
And with “latest” we choose the maximum, which is also associative:
// b > a > c
max(max(a, b), c) = b
max(a, max(b, c)) = b
The final method, “get” was not so clear. We don’t have to think too hard about it though, we can just use property-based tests to find out. Our property should look something like:
forall a b c key. append(append(a, b), c).get(key, None) = append(a, append(b, c)).get(key, None)
Meaning that to test the “get” method, we need 3 event storage instances and a key. For a property-based test, we need a way to generate the inputs. To generate an event storage instance, we just need to generate a list of events:
def genEvent[KK: Arbitrary, S: Arbitrary, E: Arbitrary]: Gen[Event[KK, S, E]] =
for {
key <- arbitrary[KK]
seq <- arbitrary[S]
instant <- Gen.posNum[Long]
operation <- arbitrary[E]
} yield Event(EventId(key, seq), new DateTime(instant, DateTimeZone.UTC), operation)
Gen.listOf(genEvent[KK, S, E]).map { events =>
new EventStorage[SafeCatchable, KK, S, E] {
def get(key: KK, fromSeq: Option[S]): Process[SafeCatchable, Event[KK, S, E]] =
Process.emitAll(events)
// Simple stubs, for now
def put(event: Event[KK, S, E]): SafeCatchable[EventStreamError / Event[KK, S, E]] =
mempty
def latest(key: KK): OptionT[SafeCatchable, Event[KK, S, E]] =
mempty
}
}
Now we can translate the property stated above into ScalaCheck:
Prop.forAll { (s1: TestEventStorage[KK, S, E], s2: TestEventStorage[KK, S, E], s3: TestEventStorage[KK, S, E], key: KK) =>
val go = get[SafeCatchable, KK, S, E](key) _
go((s1.run |+| s2.run) |+| s3.run) must equal(go(s1.run |+| (s2.run |+| s3.run)))
}
And executing our tests gives:
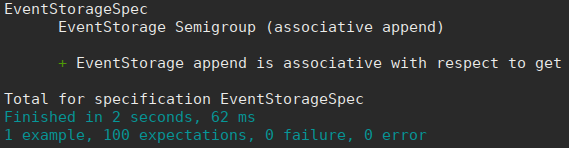
Which means we generated 100 lists of events and tested that the merging inside the “get” operation (with the tricky scalaz-stream Tee work) is associative! I could just write the operation as a Semigroup and get a lot of useful helper functions from that fact. Easy.
But there’s a lot of operations which are associative. The implementation of “get” could have just returned a stream from a single storage backend, not both. It could have always returned an empty stream. Both of these implementations would have passed the property tests, among many others.
So recognising the Semigroup will allow us to reuse some functions now and in the future, but it only assures us a little bit of correctness. We need more tests.
I spent a while looking at the signature, again:
(A, A) => A
We can have any two values of the same type and get out a value of the same type. What do we get if we put the same value in both sides?
The “get” method merges two streams together, ignoring events with duplicate keys. If we give the operation the same stream, the second one should be completely ignored – leaving us with the original stream. In algebraic terms:
forall a. append(a, a) = a
Seems like a cool property but it was one I hadn’t seen before. I didn’t know what the name was. The easiest way to find it was via Twitter:
Is there a name for the following property? forall a. a • a = a
— Brian McKenna (@puffnfresh) February 12, 2016
Within a few seconds I got the answer: this property is also known as idempotence! Rúnar (coincidentally one of the authors of scalaz-stream) then tweeted a link to mathematical bands, a.k.a. idempotent semigroups. I was unfamiliar with the binary form of idempotence so this was really cool to learn!
It looked like the event storage semigroup was an idempotent one. A simple test would tell us:
Prop.forAll { (storage: TestEventStorage[KK, S, E], key: KK) =>
val a = storage.run
val go = get[SafeCatchable, KK, S, E](key) _
go(a) must equal(go(a |+| a))
}
And ScalaCheck tells us it’s not!
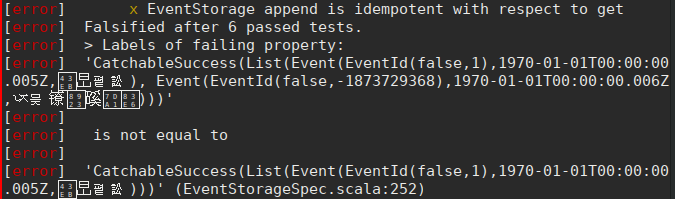
But what we see is that ScalaCheck expected to see event #1 followed by event #-1873729368 – the problem here is that the merging function assumes that all of our streams are in ascending order. It was something we had never written down before, but all of our instances should make sure they give back results in ascending order. We rely on this – so this property made us turn an assumption into a requirement!
After adding the requirement as a comment on the API, it was time to change the generator:
Gen.listOf(TestEvent.genEvent[KK, S, E]).map { list =>
val sorted = orderBy(list)(_.id.seq)
sorted
}
And now:
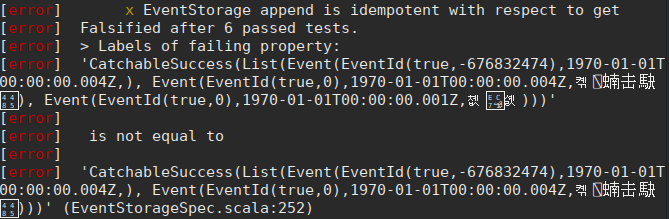
We get an error because we’re generating events in a single stream with duplicate keys. Urgh, that shouldn’t happen either. Need to be more specific with our comments and generators:
Gen.listOf(TestEvent.genEvent[KK, S, E]).map { list =>
val sorted = orderBy(list)(_.id.seq)
val unique = nubBy(sorted)(_.id.seq === _.id.seq)
unique
}
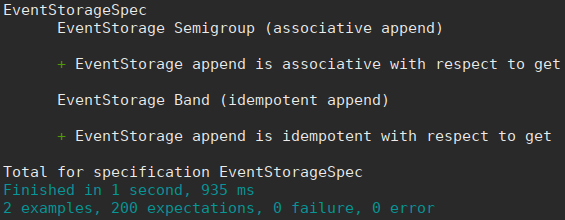
That was it!
This idempotency property doesn’t give a huge amount of reusable functions (it’s more of a performance improvement) but it does rule out “get” from always returning an empty stream. I think the biggest advantage we got from this is a refined requirement on the API.
Since we’re now saying that the API has requirements of being sorted and distinct, we should explicitly test that the requirements are upheld after being put through the Semigroup operation:
// Stream elements are in ascending order
Prop.forAll { (s1: TestEventStorage[KK, S, E], s2: TestEventStorage[KK, S, E], key: KK) =>
val go = get[SafeCatchable, KK, S, E](key) _
go(s1.run |+| s2.run).map(orderBy(_)((_: Event[KK, S, E]).id.seq)) must equal(go(s1.run |+| s2.run))
}
// Stream elements are distinct
Prop.forAll { (s1: TestEventStorage[KK, S, E], s2: TestEventStorage[KK, S, E], key: KK) =>
val go = get[SafeCatchable, KK, S, E](key)(_: EventStorage[SafeCatchable, KK, S, E]).get
val result = go(s1.run |+| s2.run)
nubBy(result)(_ === _) must equal(result)
}
And finally, to make sure we’re totally correct, we should test that our scalaz-stream Tee-based combining function is the same as a very inefficient, but simple, list-based approach:
Prop.forAll { (s1: TestEventStorage[KK, S, E], s2: TestEventStorage[KK, S, E], key: KK) =>
val go = get[SafeCatchable, KK, S, E](key) _
val xs = s1.underlyingGet ++ s2.underlyingGet
val filtered = xs.filter(_.id.key === key)
val sorted = orderBy(filtered)((_: Event[KK, S, E]).id.seq)
val unique = nubBy(sorted)(_.id === _.id)
unique must equal(go(s1.run |+| s2.run).get)
}
Now we can be confident that “get” is correct. We can go through and do the simple “put” and “latest” cases. We end up with the following:
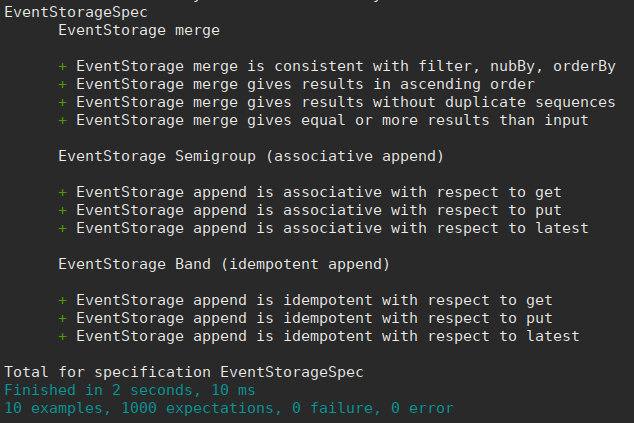
That’s 1000 tests, taking just a couple of seconds to run! We know that eventsrc’s stream combining is rock solid without knowing anything about the scalaz-stream Tee algorithm and without having any integration tests.

There’s still a couple of algebraic properties we should look into. Either for reusability, extra correctness guarantees, optimisations, reasoning tools or even just as exercises!
- We get close to a Monoid (both “get” and “latest” have empty elements, “put” might need something extra to make an empty element)
- The Band seems like it is a “left-regular band” which means the following should hold:
append(a, append(b, a)) = a
If you are interested in doing this, I will help you out as much as you need. Take a look at the outcome of our work on Bitbucket.
Talk algebraic programming with me at @puffnfresh and follow us on @atlassiandev.